철솜_STUDY
파이썬 머신러닝 완벽 가이드 _CH.6 본문
CH.6.1 _ 차원 축소 개요
차원 축소는 고차원의 데이터 세트가 저차원의 데이터 세트에 비해 예측 신뢰도가 떨어진다는 단점을 해결하기 위한 개념이다.피처의 수가 많을 수록 예측 신뢰도가 떨어지고, 개별 피처 간의 상관관계가 높다는 점을 이용해 피처의 수를 줄인다
차원 축소 방법은 크게 두 가지로 나뉜다.타 피처에 대한 종속성이 높은 피처를 제거하는 '피처 선택' 방법과, 기존 피처를 저차원으로 압축하는 '피처 추출' 방식이다.후자 피처 추출 방식의 경우, 단순히 피처를 저차원으로 줄이는 것이 아니라, 해당 데이터 세트를 더 잘 설명할 수 있는 잠재요소 'Latent factor'를 추출한다는 점에서 유의미하다.
이러한 차원 축소의 개념을 구현하는 방법이 차원 축소 알고리즘으로 PCA, LDA, SVD, NMF가 있다.PCA와 LDA는 서로 유사한 개념이다.
차원 축소 알고리즘이 사용되는 대표적인 예시가 이미지 데이터와 텍스트 문서 의미 분석이다.이미지 데이터의 경우 매우 많은 픽셀로 이뤄져 있기 때문에, 이런 고차원의 피처에 잠재된 특성을 피처로 도출해 함축적 형태의 이미지 변환과 압축을 진행하게 된다. 앞서 말했다시피 차원이 적어졌기 때문에 과적합의 영향력이 작아져 예측 성능이 증가하는 효과가 나타난다.텍스트 의미 분석의 경우, 많은 단어로 구성됐다는 점, 문서를 만드는 사람이 어떤 의미나 의도를 가지고 작성한다는 점에서 문서 내 단어의 구성에 잠재된 Semantic 의미나 Topic을 잠재 요소로 간주하고 찾아내게 된다. 이러한 상황에 기반이 되는 알고리즘이 바로 SVD와 NMF이다.
CH.6.2 _ PCA : Pricipal Component Analysis
PCA는 여러 변수 간의 상관관계를 이용해 주성분_principal component를 추출하는 방식이다.
기존 데이터의 정보 손실을 최소화 하기 위해 분산을 이용하게 된다.
가장 높은 분산을 가지는 데이터 축을 찾아 해당 축으로 데이터를 투영해 차원을 축소하는 것이다.
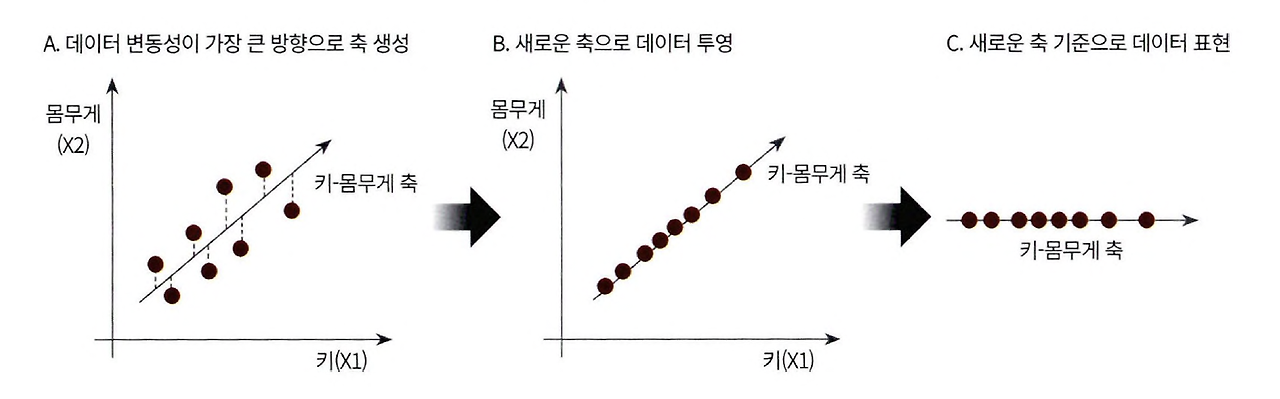
위의 예시는 하나의 축을 생성하는 과정을 보여주고 있다.
PCA는 여러 개의 축을 만들 때는 위의 과정을 통해 첫 번째 벡터 축을 만들고, 두 번째 축은 첫 번째 벡터 축에 직각이 되는 벡터로, 세 번째는 두 번째 벡터 축에 직각이 되는 벡터로 한다.
PCA 과정을 선형대수적으로 해석하면 다음과 같다.
입력 데이터의 공분산 행렬 -----------------------> 고유 벡터 = PCA의 주성분 벡터** --------------------> 새로운 공간으로 투영
by.고유값* 분해 by. 선형변환***
*고유값은 eigne value로 고유벡터의 크기이자, 입력 데이터의 분산을 나타낸다.
**주성분 벡터는 입력 데이터의 분산이 큰 방향을 나타낸다.
***선형변환은 벡터A * 행렬B = 벡터C 가 되는 것으로, 벡터 A를 벡터 C로 만들어서 새로운 공간으로 투영하는 것이다.
>>> 행렬을 공간으로 가정한다는 내용이 잘 이해가 가지 않는다. 추가적으로 찾아보기.
결론을 말하면 입력 데이터의 공분산 행렬은 고유벡터와 고유값으로 분해될 수 있다는 것이 이 PCA의 핵심적인 내용이다.
PCA 과정
1. 입력 데이터 세트의 공분산 행렬 생성
2. 공분산 행렬의 고유벡터와 고유값 계산
3. 고유값이 큰 순으로 K개만큼 고유벡터 추출
4. 고유값이 큰 순으로 추출된 고유벡터를 이용해 입력 데이터 변환
from sklearn.datasets import load_iris
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
##4개의 속성을 2개의 PCA 차원으로 압축해 비교하는 것
iris = load_iris()
columns = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
irisDF = pd.DataFrame(iris.data, columns=columns)
irisDF['target'] = iris.target
#원본 세트 분포 시각화
markers=['^', 's', 'o']
for i, marker in enumerate(markers):
x_axis_data = irisDF[irisDF['target']==i]['sepal_length']
y_axis_data = irisDF[irisDF['target']==i]['sepal_width']
plt.scatter(x_axis_data, y_axis_data, marker=marker, label=iris.target_names[i])
plt.legend()
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.show()
##
from sklearn.preprocessing import StandardScaler
iris_scaled = StandardScaler().fit_transform(irisDF.iloc[:,:-1])
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(iris_scaled)
iris_pca = pca.transform(iris_scaled)
print(iris_pca.shape)
###
pca_columns = ['pca_component_1', 'pca_component_2']
irisDF_pca = pd.DataFrame(iris_pca, columns=pca_columns)
irisDF_pca['target'] = iris.target
irisDF_pca.head(3)
markers=['^', 's', 'o']
for i, marker in enumerate(markers):
x_axis_data = irisDF_pca[irisDF_pca['target']==i]['pca_component_1' ]
y_axis_data = irisDF_pca[irisDF_pca['target']==i][ 'pca_component_2']
plt.scatter(x_axis_data, y_axis_data, marker=marker, label=iris.target_names[i])
plt.legend()
plt.xlabel('pca_component_1')
plt.ylabel('pca_component_2')
plt.show()from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
import numpy as np
rcf = RandomForestClassifier(random_state=156)
scores = cross_val_score(rcf, iris.data, iris.target, scoring='accuracy', cv=3)
print('원본 데이터 교차 검증 개별 정확도: ', scores)
print('원본 데이터 평균 정확도: ', np.mean(scores))
##
pca_X = irisDF_pca[['pca_component_1', 'pca_component_2']]
scores_pca = cross_val_score(rcf, pca_X, iris.target, scoring='accuracy', cv=3)
print('원본 데이터 교차 검증 개별 정확도: ', scores_pca)
print('원본 데이터 평균 정확도: ', np.mean(scores_pca))
원본 데이터 교차 검증 개별 정확도: [0.98 0.94 0.96]
원본 데이터 평균 정확도: 0.96원본 데이터 교차 검증 개별 정확도: [0.88 0.88 0.88]
원본 데이터 평균 정확도: 0.88## 2번째 예제
import pandas as pd
df = pd.read_excel("C:\\ext\\default+of+credit+card+clients\\default of credit card clients.xls", header=1, sheet_name='Data').iloc[0:,1:]
print(df.shape)
df.head(3)
df.rename(columns={'PAY_0':'PAY_1', 'default payment next month':'default'}, inplace=True)
y_target=df['default']
X_features = df.drop('default', axis=1)
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
corr = X_features.corr()
plt.figure(figsize=(14,14))
sns.heatmap(corr, annot=True, fmt='.1g')
##변수들 간의 상관성 파악
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
cols_bill=['BILL_AMT'+str(i) for i in range(1,7)]
print('대상 속성 명:', cols_bill)
scaler = StandardScaler()
df_cols_scaled = scaler.fit_transform(X_features[cols_bill])
pca=PCA(n_components=2)
pca.fit(df_cols_scaled)
print('PCA component별 변동성: ', pca.explained_variance_ratio_)
대상 속성 명: ['BILL_AMT1', 'BILL_AMT2', 'BILL_AMT3', 'BILL_AMT4', 'BILL_AMT5', 'BILL_AMT6']
PCA component별 변동성: [0.90555253 0.0509867 ]import numpy as np
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
rcf = RandomForestClassifier(n_estimators=300, random_state=156)
scores = cross_val_score(rcf, X_features, y_target, scoring='accuracy', cv=3)
print('CV=3인 경우의 개별 Fold 세트 별 정확도: ', scores)
print('평균 정확도: {0:.4f}'.format(np.mean(scores)))
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
df_scaled = scaler.fit_transform(X_features)
pca=PCA(n_components=6)
df_pca = pca.fit_transform(df_scaled)
scores_pca = cross_val_score(rcf, df_pca, y_target, scoring='accuracy', cv=3)
print('CV=3인 경우의 개별 Fold 세트 별 정확도: ', scores)
print('평균 정확도: {0:.4f}'.format(np.mean(scores)))CV=3인 경우의 개별 Fold 세트 별 정확도: [0.8083 0.8196 0.8232]
평균 정확도: 0.8170CV=3인 경우의 개별 Fold 세트 별 정확도: [0.7901 0.7973 0.8029]
평균 정확도: 0.7968CH.6.3 _ LDA : Linear Discriminant Analysis
LDA는 PCA와 많은 지점에서 유사하지만 지도학습의 분류에 더 적절하다.
LDA는 분류에서 사용하기 윕도록 개별 클래스를 분별할 수 잇는 기준을 최대한 유지하면서 축소한다.
즉, 입력 데이터의 결정 값 클래스를 최대한으로 분리할 수 있는 축을 찾는다.
LDA는 공간 상에서 클래스 분리를 최대화하는 축을 찾기 위해 클래스 간 분산과 클래스 내부 분산의 비율을 최대화하는 방식으로 차원을 축소한다. 클래스 간의 분산은 최대한 크게, 클래스 내부의 분산은 최대한 길게 가져가는 방식.
LDA 과정
1. 입력 데이터 세트의 클래스 간 분산과 클래스 내부 분산 행렬 생성
_입력 데이터의 결정 값 클래스별로 개별 피처의 평균 벡터를 기반으로
2. 이 행렬들의 고유벡터와 고유값 계산
3. 고유값이 큰 순으로 K개만큼 고유벡터 추출
4. 고유값이 큰 순으로 추출된 고유벡터를 이용해 입력 데이터 변환
## LDA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
iris = load_iris()
iris_scaled = StandardScaler().fit_transform(iris.data)
lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(iris_scaled, iris.target)
iris_lda = lda.transform(iris_scaled)
print(iris_lda.shape)
from sklearn.datasets import load_iris
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
##4개의 속성을 2개의 PCA 차원으로 압축해 비교하는 것
lda_columns = ['lda_component_1', 'lda_component_2']
irisDF_lda = pd.DataFrame(iris_lda, columns=lda_columns)
irisDF_lda['target'] = iris.target
#원본 세트 분포 시각화
markers=['^', 's', 'o']
for i, marker in enumerate(markers):
x_axis_data = irisDF_lda[irisDF_lda['target']==i]['lda_component_1']
y_axis_data = irisDF_lda[irisDF_lda['target']==i]['lda_component_2']
plt.scatter(x_axis_data, y_axis_data, marker=marker, label=iris.target_names[i])
plt.legend(loc='upper right')
plt.xlabel('lda_component_1')
plt.ylabel('lda_component_2')
plt.show()
CH.6.4 _ SVD : Singular Value Decomposition
SVD는 PCA와 달리 행과 열의 크기가 다른 행렬에 적용이 가능한 행렬 분해 기법이다.

U, V = singular vector _ 특이 벡터
시그마 = 대각 행렬 : 대각 성분을 제외하고 나머지는 모두 0이다. 대각 성분이 행렬 A의 특이값이 되는데,
그 중 특이값이 0인 것들을 제외하게 된다.
이후 시그마의 대각원소 중 상위 몇 개만 추출해서 이에 대응하는 U, V를 제거해 차원을 줄인 형태로 분해하게 된다. 이것이 Truncated SVD이다.
import numpy as np
from numpy.linalg import svd
np.random.seed(121)
a = np.random.randn(4,4)
print(np.round(a,3))
## U, sigma, Vt 추출
U, Sigma, Vt = svd(a)
print(U.shape, Sigma.shape, Vt.shape)
print('U matrix: \n', np.round(U, 3))
print('Sigma matrix: \n', np.round(Sigma, 3))
print('Vt matrix: \n', np.round(Vt, 3))
sigma_mat = np.diag(Sigma)
a_ = np.dot(np.dot(U,sigma_mat), Vt)
print(np.round(a_,3))[[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.014 0.63 1.71 -1.327]
[ 0.402 -0.191 1.404 -1.969]](4, 4) (4,) (4, 4)
U matrix:
[[-0.079 -0.318 0.867 0.376]
[ 0.383 0.787 0.12 0.469]
[ 0.656 0.022 0.357 -0.664]
[ 0.645 -0.529 -0.328 0.444]]
Sigma matrix:
[3.423 2.023 0.463 0.079]
Vt matrix:
[[ 0.041 0.224 0.786 -0.574]
[-0.2 0.562 0.37 0.712]
[-0.778 0.395 -0.333 -0.357]
[-0.593 -0.692 0.366 0.189]][[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.014 0.63 1.71 -1.327]
[ 0.402 -0.191 1.404 -1.969]]##로우 간 의존성에 대한 내용 확인
a[2]=a[0]+a[1]
a[3]=a[0]
print(np.round(a,3))
U, Sigma, Vt = svd(a)
print(U.shape, Sigma.shape, Vt.shape)
print('Sigma matrix: \n', np.round(Sigma, 3))
## 특이 행렬의 4 원소 중 2개의 값이 0 ==> 선형 독립인 로우 벡터의 개수가 2개라는 의미임 즉, 행렬의 Rank=2라는 의미
U_ = U[:,:2]
Sigma_ = np.diag(Sigma[:2])
Vt_ = Vt[:2]
print(U_.shape, Sigma_.shape, Vt_.shape)
a_ = np.dot(np.dot(U_, Sigma_), Vt_)
print(np.round(a_,3))[[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.542 0.899 1.041 -0.073]
[-0.212 -0.285 -0.574 -0.44 ]](4, 4) (4,) (4, 4)
Sigma matrix:
[2.663 0.807 0. 0. ](4, 2) (2, 2) (2, 4)
[[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.542 0.899 1.041 -0.073]
[-0.212 -0.285 -0.574 -0.44 ]]## Truncated SVD
import numpy as np
from scipy.sparse.linalg import svds
from scipy.linalg import svd
np.random.seed(121)
matrix = np.random.random((6,6))
print('원본 행렬 : \n', matrix)
U, Sigma, Vt = svd(matrix, full_matrices = False)
print('\n분해 행렬 차원 :', U.shape, Sigma.shape, Vt.shape)
print('\nSigma값 행렬 : ', Sigma)
num_components=4
U_tr, Sigma_tr, Vt_tr = svds(matrix, k=num_components)
print('\nTruncated SVD 분해 행렬 차원 :', U_tr.shape, Sigma_tr.shape, Vt_tr.shape)
print('\nTruncated SVD Sigma 값 행렬 : ', Sigma_tr )
matrix_tr = np.dot(np.dot(U_tr, np.diag(Sigma_tr)), Vt_tr)
print('\nTruncated SVD로 분해 후 복원 행렬 : \n', matrix_tr)
from sklearn.decomposition import TruncatedSVD, PCA
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
%matplotlib inline
iris = load_iris()
iris_ftrs = iris.data
tsvd = TruncatedSVD(n_components=2)
tsvd.fit(iris_ftrs)
iris_tsvd = tsvd.transform(iris_ftrs)
plt.scatter(x=iris_tsvd[:, 0], y=iris_tsvd[:, 1], c=iris.target)
plt.xlabel('TruncatedSVD Component 1')
plt.ylabel('TruncatedSVD Component 2')
from sklearn.preprocessing import StandardScaler
scaler=StandardScaler()
iris_scaled=scaler.fit_transform(iris_ftrs)
tsvd = TruncatedSVD(n_components=2)
tsvd.fit(iris_scaled)
iris_tsvd = tsvd.transform(iris_scaled)
pca = PCA(n_components=2)
pca.fit(iris_scaled)
iris_pca = pca.transform(iris_scaled)
fig, (ax1, ax2) = plt.subplots(figsize=(9,4), ncols=2)
ax1.scatter(x=iris_tsvd[:, 0], y=iris_tsvd[:, 1], c=iris.target)
ax2.scatter(x=iris_pca[:, 0], y=iris_pca[:, 1], c=iris.target)
ax1.set_title('Truncated SVD Transformed')
ax2.set_title('PCA Transformed')
원본 행렬 :
[[0.11133083 0.21076757 0.23296249 0.15194456 0.83017814 0.40791941]
[0.5557906 0.74552394 0.24849976 0.9686594 0.95268418 0.48984885]
[0.01829731 0.85760612 0.40493829 0.62247394 0.29537149 0.92958852]
[0.4056155 0.56730065 0.24575605 0.22573721 0.03827786 0.58098021]
[0.82925331 0.77326256 0.94693849 0.73632338 0.67328275 0.74517176]
[0.51161442 0.46920965 0.6439515 0.82081228 0.14548493 0.01806415]]
분해 행렬 차원 : (6, 6) (6,) (6, 6)
Sigma값 행렬 : [3.2535007 0.88116505 0.83865238 0.55463089 0.35834824 0.0349925 ]
Truncated SVD 분해 행렬 차원 : (6, 4) (4,) (4, 6)
Truncated SVD Sigma 값 행렬 : [0.55463089 0.83865238 0.88116505 3.2535007 ]
Truncated SVD로 분해 후 복원 행렬 :
[[0.19222941 0.21792946 0.15951023 0.14084013 0.81641405 0.42533093]
[0.44874275 0.72204422 0.34594106 0.99148577 0.96866325 0.4754868 ]
[0.12656662 0.88860729 0.30625735 0.59517439 0.28036734 0.93961948]
[0.23989012 0.51026588 0.39697353 0.27308905 0.05971563 0.57156395]
[0.83806144 0.78847467 0.93868685 0.72673231 0.6740867 0.73812389]
[0.59726589 0.47953891 0.56613544 0.80746028 0.13135039 0.03479656]]


CH.6.5 _ NMF : Non-Negative Matrix Factorization
NMF는 Truncated SVD와 같이 낮은 랭크를 통한 행렬 근사 방식의 변형이다.
원본 행렬 V의 모든 원소 값이 양수라는 것이 보장되면 V=W*H 처럼 분해할 수 있는 기법이다.
행렬 분해는 SVD와 같은 행렬 분해 기법을 통칭하는 것으로, 행렬 분해를 하게 되면 길고 가는 W, 작고 넓은 H로 분해되는데, 잠재 요소를 특성으로 가지게 된다.
from sklearn.decomposition import NMF
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
%matplotlib inline
iris=load_iris()
iris_ftrs = iris.data
nmf = NMF(n_components=2)
nmf.fit(iris_ftrs)
iris_nmf = nmf.transform(iris_ftrs)
plt.scatter(x=iris_nmf[:, 0], y=iris_nmf[:,1], c=iris.target)
plt.xlabel('NMF Component 1')
plt.ylabel('NMF Component 2')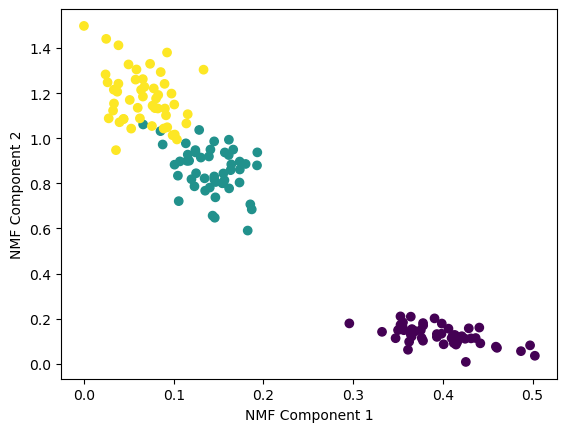
CH.6.6 _ 정리
차원 축소는 단순히 피처의 개수를 줄이는 개념이 아니라 이를 통해 데이터를 더 잘 설명할 수 있는 잠재적인 요소를 추출하는데 의미가 있다.
PCA는 입력 데이터의 변동성이 가장 큰 축을 구하고, 다시 이 축에 직각인 축을 반복적으로 축소하려는 차원 개수만큼 구한 뒤 입력 데이터를 이 축에 투영해 차원을 축소하는 방식이다.
이를 위해 공분산 행렬을 기반으로 고유 벡터를 생성하고, 해당 고유 벡터에 입력 데이터를 선형 변환하게 된다.
LDA는 PCA와 유사하지만, 입력 데이터의 결정 값 클래스를 최대한으로 분리할 수 있는 축을 찾는 방식으로 차원을 축소한다.
SVD와 NMF는 매우 많은 피처를 가진 고차원 행렬을 두 개의 저차원 행렬로 분리하는 기법이다.
원본 행렬에 잠재된 요소를 추출하기 때문에 토픽 모델링이나 추천 시스템에서 사용된다.
'Self-Taught > Machine Learning' 카테고리의 다른 글
| 머신러닝 완벽 가이드 _ CH.8 : 텍스트 분석 (2) (2) | 2024.12.26 |
|---|---|
| 머신러닝 완벽 가이드 _ CH.7 : 군집화 (1) | 2024.11.30 |
| 파이썬 머신러닝 완벽 가이드 _CH.5 (0) | 2024.11.16 |
| 파이썬 머신러닝 완벽 가이드 _ CH.4.7~4.12 (1) | 2024.11.09 |
| 파이썬 머신러닝 완벽 가이드 _ CH.4.1~4.6 (1) | 2024.11.02 |




